NMR determined Rotational correlation time: Difference between revisions
(Created page with '== '''Introduction''' == The rotational correlation time of a protein in solution is the time for a protein to rotate one radian. In the limit of slow molecular motion (τ<sub>…') |
No edit summary |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
[[Image:T1wiki fig5.png|right|400px]] Brownian rotation diffusion of a particle in solution has a characteristic time constant called rotational correlation time (τ<sub>c</sub>). It is the time it takes the particle to rotate by one radian and it depends on the particle size. For globular proteins a spherical approximation can be used and the rotational correlation time is given by Stoke's law | |||
:<math>\tau_c=\frac{4\pi\eta r^3}{3kT}</math>, | |||
where <span class="texhtml">η</span> is the viscosity of the solvent, <span class="texhtml">''r''</span> is the effective hydrodynamic radius of the protein molecule, <span class="texhtml">''k''</span> is the Boltzmann constant and <span class="texhtml">''T''</span> is the temperature. The hydrodynamic radius can be estimated from the molecular weight of the protein (M) as | |||
:<math>r\approx\sqrt[3]{\frac{3M}{4\pi\rho N_a}}+r_w</math>, | |||
where <span class="texhtml">ρ</span> is the average density for proteins (1.37 g/cm3), <span class="texhtml">''N''<sub>''a''</sub></span> is the Avogadro's number and <span class="texhtml">''r''<sub>''w''</sub></span> is the hydration radius (1.6 to 3.2 A)<ref>Cavanagh J., Fairbrother W.J., Palmer, A.G, Rance M., Skelton N.J. (2007) Protein NMR Spectroscopy: Principles and Practice, p21, Elsevier</ref>. As a general rule of thumb, the τ<sub>c</sub> of a monomeric protein in solution in nanoseconds is approximately 0.6 times its molecular weight in kDa. | |||
<br> | <br> | ||
For rigid protein molecules, in the limit of slow molecular motion (τ<sub>c</sub> >> 0.5 ns) and high magnetic field (500 MHz or greater), a closed-form solution for τ<sub>c</sub> as a function of the ratio of the longitudinal (T<sub>1</sub>) and transverse (T<sub>2</sub>) <sup>15</sup>N relaxation times exists: | |||
:<math>\tau_c\approx\frac{1}{4\pi\nu_N}\sqrt{6\frac{T_1}{T_2}-7}</math>, | |||
* | where ν<sub>N</sub> is the <sup>15</sup>N resonance frequency (in Hz). This equation is derived from Eq. 8 in ref.<ref><pubmed>2690953</pubmed></ref> by considering only J(0) and J(ωN) spectral density terms and neglecting higher frequency terms. | ||
<br> | <br> Average <sup>15</sup>N T<sub>1</sub> and T<sub>2</sub> relaxation times for a given protein can be measured using 1D <sup>15</sup>N-edited relaxation experiments <ref><pubmed>7514039</pubmed></ref>. To minimize contributions from unfolded segments each 1D spectum is integrated over the downfield backbone amide <sup>1</sup>H region (typically 10.5 to 8.5 ppm) and the results are used to fit an exponential decay as a function of delay time. One then computes the correlation time using Eq. 3, and compares it to a standard curve of τ<sub>c</sub> vs. protein molecular weight (MW) obtained at the same temperature on a series of known monomeric proteins of varying size. The T<sub>1</sub>/T<sub>2</sub> method is suitable for proteins with molecular weight of up to MW ≈ 25 kDa. Accurate measurement of the diminishing <sup>15</sup>N T<sub>2</sub> becomes difficult for larger proteins and cross-correlated relaxation rates are measured instead. | ||
== <span class="mw-headline">''' | |||
<br> | |||
Below is a table of rotational correlation time values compiled for known monomeric NESG targets (J. Aramini; June 2010). All data was recorded on a Bruker 600 NMR instrument at 298 K. The molecular weight for each target takes into account isotopic enrichment and the presence of affinity purification tags (if any). | |||
<br> | |||
{| cellspacing="1" cellpadding="1" border="1" align="center" style="width: 1047px; height: 393px;" | |||
|- | |||
| width="250" align="center" | '''NESG target (isotope labeling)''' | |||
| align="center" | '''MW (kDa)''' | |||
| align="center" | '''<sup>15</sup>N ''T<sub></sub>''<sub>1</sub> (ms)''' | |||
| align="center" | '''<sup>15</sup>N ''T''<sub>2</sub> (ms)''' | |||
| align="center" | '''τ<sub>c</sub> (ns)''' | |||
|- | |||
| width="250" align="center" | PsR76A (NC5) | |||
| align="center" | 7.2 | |||
| align="center" | 478.0 | |||
| align="center" | 128.0 | |||
| align="center" | 5.10 | |||
|- | |||
| width="250" align="center" | VfR117 (NC) | |||
| align="center" | 11.2 | |||
| align="center" | 605.0 | |||
| align="center" | 119.0 | |||
| align="center" | 6.30 | |||
|- | |||
| width="250" align="center" | SyR11 (NC5) | |||
| align="center" | 12.4 | |||
| align="center" | 630.0 | |||
| align="center" | 104.0 | |||
| align="center" | 7.10 | |||
|- | |||
| width="250" align="center" | ER541-37-162 (NC5) | |||
| align="center" | 15.8 | |||
| align="center" | 729.0 | |||
| align="center" | 66.5 | |||
| align="center" | 10.0 | |||
|- | |||
| width="250" align="center" | ER540 (NC5) | |||
| align="center" | 18.8 | |||
| align="center" | 909.0 | |||
| align="center" | 66.5 | |||
| align="center" | 11.3 | |||
|- | |||
| width="250" align="center" | SoR190 (NC) | |||
| align="center" | 13.8 | |||
| align="center" | 697.5 | |||
| align="center" | 100.9 | |||
| align="center" | 7.70 | |||
|- | |||
| width="250" align="center" | TR80 (NC5) | |||
| align="center" | 10.5 | |||
| align="center" | 612.8 | |||
| align="center" | 102.9 | |||
| align="center" | 7.00 | |||
|- | |||
| width="250" align="center" | Ubiquitin (NC) | |||
| align="center" | 9.0 | |||
| align="center" | 441.8 | |||
| align="center" | 144.6 | |||
| align="center" | 4.40 | |||
|- | |||
| width="250" align="center" | HR2873B (NC) | |||
| align="center" | 10.7 | |||
| align="center" | 492.0 | |||
| align="center" | 115.0 | |||
| align="center" | 5.70 | |||
|- | |||
| width="250" align="center" | B-domain (NC) | |||
| align="center" | 7.2 | |||
| align="center" | 423.5 | |||
| align="center" | 153.3 | |||
| align="center" | 4.05 | |||
|- | |||
| width="250" align="center" | BcR97A (NC) | |||
| align="center" | 13.1 | |||
| align="center" | 705.8 | |||
| align="center" | 80.6 | |||
| align="center" | 8.80 | |||
|- | |||
| width="250" align="center" | PfR193A (NC) | |||
| align="center" | 13.6 | |||
| align="center" | 733.9 | |||
| align="center" | 80.9 | |||
| align="center" | 9.00 | |||
|- | |||
| width="250" align="center" | MvR76 (NC) | |||
| align="center" | 20.2 | |||
| align="center" | 1015.0 | |||
| align="center" | 64.5 | |||
| align="center" | 12.2 | |||
|- | |||
| width="250" align="center" | DvR115G (NC) | |||
| align="center" | 10.9 | |||
| align="center" | 608.7 | |||
| align="center" | 115.6 | |||
| align="center" | 6.50 | |||
|- | |||
| width="250" align="center" | MrR110B (NC5) | |||
| align="center" | 11.8 | |||
| align="center" | 707.0 | |||
| align="center" | 99.2 | |||
| align="center" | 7.80 | |||
|- | |||
| width="250" align="center" | VpR247 (NC5) | |||
| align="center" | 12.5 | |||
| align="center" | 661.2 | |||
| align="center" | 88.3 | |||
| align="center" | 8.05 | |||
|- | |||
| width="250" align="center" | BcR147A (NC) | |||
| align="center" | 11.9 | |||
| align="center" | 645.0 | |||
| align="center" | 104.0 | |||
| align="center" | 7.20 | |||
|- | |||
| width="250" align="center" | WR73 (NC5) | |||
| align="center" | 21.9 | |||
| align="center" | 1261.0 * | |||
| align="center" | 41.3 * | |||
| align="center" | 13.0 | |||
|- | |||
| width="250" align="center" | NsR431C (NC5) | |||
| align="center" | 16.8 | |||
| align="center" | 855.5 | |||
| align="center" | 71.2 | |||
| align="center" | 10.6 | |||
|- | |||
| width="250" align="center" | StR82 (NC) | |||
| align="center" | 9.2 | |||
| align="center" | 537.3 | |||
| align="center" | 100.4 | |||
| align="center" | 6.6 | |||
|} | |||
*data obtained on an 800 MHz Bruker spectrometer at 298 K. | |||
<br> | |||
== <span class="mw-headline">'''Protocols for Bruker and Varian NMR Instruments'''</span> == | |||
*[[Measuring 15N T1 and T2 Relaxation Times on Bruker Instruments|Bruker protocol]] | |||
*[[Estimation of rotational correlation time|Varian protocol]] | |||
<br> | <br> | ||
- | == <span class="mw-headline">'''References''' </span> == | ||
<references /> | |||
Latest revision as of 22:43, 13 October 2011
Brownian rotation diffusion of a particle in solution has a characteristic time constant called rotational correlation time (τc). It is the time it takes the particle to rotate by one radian and it depends on the particle size. For globular proteins a spherical approximation can be used and the rotational correlation time is given by Stoke's law
- <math>\tau_c=\frac{4\pi\eta r^3}{3kT}</math>,
where η is the viscosity of the solvent, r is the effective hydrodynamic radius of the protein molecule, k is the Boltzmann constant and T is the temperature. The hydrodynamic radius can be estimated from the molecular weight of the protein (M) as
- <math>r\approx\sqrt[3]{\frac{3M}{4\pi\rho N_a}}+r_w</math>,
where ρ is the average density for proteins (1.37 g/cm3), Na is the Avogadro's number and rw is the hydration radius (1.6 to 3.2 A)[1]. As a general rule of thumb, the τc of a monomeric protein in solution in nanoseconds is approximately 0.6 times its molecular weight in kDa.
For rigid protein molecules, in the limit of slow molecular motion (τc >> 0.5 ns) and high magnetic field (500 MHz or greater), a closed-form solution for τc as a function of the ratio of the longitudinal (T1) and transverse (T2) 15N relaxation times exists:
- <math>\tau_c\approx\frac{1}{4\pi\nu_N}\sqrt{6\frac{T_1}{T_2}-7}</math>,
where νN is the 15N resonance frequency (in Hz). This equation is derived from Eq. 8 in ref.[2] by considering only J(0) and J(ωN) spectral density terms and neglecting higher frequency terms.
Average 15N T1 and T2 relaxation times for a given protein can be measured using 1D 15N-edited relaxation experiments [3]. To minimize contributions from unfolded segments each 1D spectum is integrated over the downfield backbone amide 1H region (typically 10.5 to 8.5 ppm) and the results are used to fit an exponential decay as a function of delay time. One then computes the correlation time using Eq. 3, and compares it to a standard curve of τc vs. protein molecular weight (MW) obtained at the same temperature on a series of known monomeric proteins of varying size. The T1/T2 method is suitable for proteins with molecular weight of up to MW ≈ 25 kDa. Accurate measurement of the diminishing 15N T2 becomes difficult for larger proteins and cross-correlated relaxation rates are measured instead.
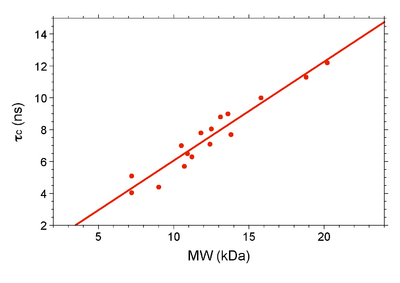
Below is a table of rotational correlation time values compiled for known monomeric NESG targets (J. Aramini; June 2010). All data was recorded on a Bruker 600 NMR instrument at 298 K. The molecular weight for each target takes into account isotopic enrichment and the presence of affinity purification tags (if any).
| NESG target (isotope labeling) | MW (kDa) | 15N T1 (ms) | 15N T2 (ms) | τc (ns) |
| PsR76A (NC5) | 7.2 | 478.0 | 128.0 | 5.10 |
| VfR117 (NC) | 11.2 | 605.0 | 119.0 | 6.30 |
| SyR11 (NC5) | 12.4 | 630.0 | 104.0 | 7.10 |
| ER541-37-162 (NC5) | 15.8 | 729.0 | 66.5 | 10.0 |
| ER540 (NC5) | 18.8 | 909.0 | 66.5 | 11.3 |
| SoR190 (NC) | 13.8 | 697.5 | 100.9 | 7.70 |
| TR80 (NC5) | 10.5 | 612.8 | 102.9 | 7.00 |
| Ubiquitin (NC) | 9.0 | 441.8 | 144.6 | 4.40 |
| HR2873B (NC) | 10.7 | 492.0 | 115.0 | 5.70 |
| B-domain (NC) | 7.2 | 423.5 | 153.3 | 4.05 |
| BcR97A (NC) | 13.1 | 705.8 | 80.6 | 8.80 |
| PfR193A (NC) | 13.6 | 733.9 | 80.9 | 9.00 |
| MvR76 (NC) | 20.2 | 1015.0 | 64.5 | 12.2 |
| DvR115G (NC) | 10.9 | 608.7 | 115.6 | 6.50 |
| MrR110B (NC5) | 11.8 | 707.0 | 99.2 | 7.80 |
| VpR247 (NC5) | 12.5 | 661.2 | 88.3 | 8.05 |
| BcR147A (NC) | 11.9 | 645.0 | 104.0 | 7.20 |
| WR73 (NC5) | 21.9 | 1261.0 * | 41.3 * | 13.0 |
| NsR431C (NC5) | 16.8 | 855.5 | 71.2 | 10.6 |
| StR82 (NC) | 9.2 | 537.3 | 100.4 | 6.6 |
- data obtained on an 800 MHz Bruker spectrometer at 298 K.
Protocols for Bruker and Varian NMR Instruments