Jmodulation Experiment RDC

NMR Data Processing >  Jmod Measurement of RDCs

Pulse Sequence (J H-N)

The sequence is modified from the fast HSQC sequence (gNfhsqc) in Varian BioPack. For details see Tjandra N. et al, JACS (1996), 118, 6364-72.   

A series of 2D experiments should be acquired with the J modulation delay (Delta) set to different values, preferably in an interleaved fashion. (Note that “Delta” is half the total modulation delay.)  For example, in Vnmr, this can be realized by:

array(‘Delta’,8,0.002,0.002)

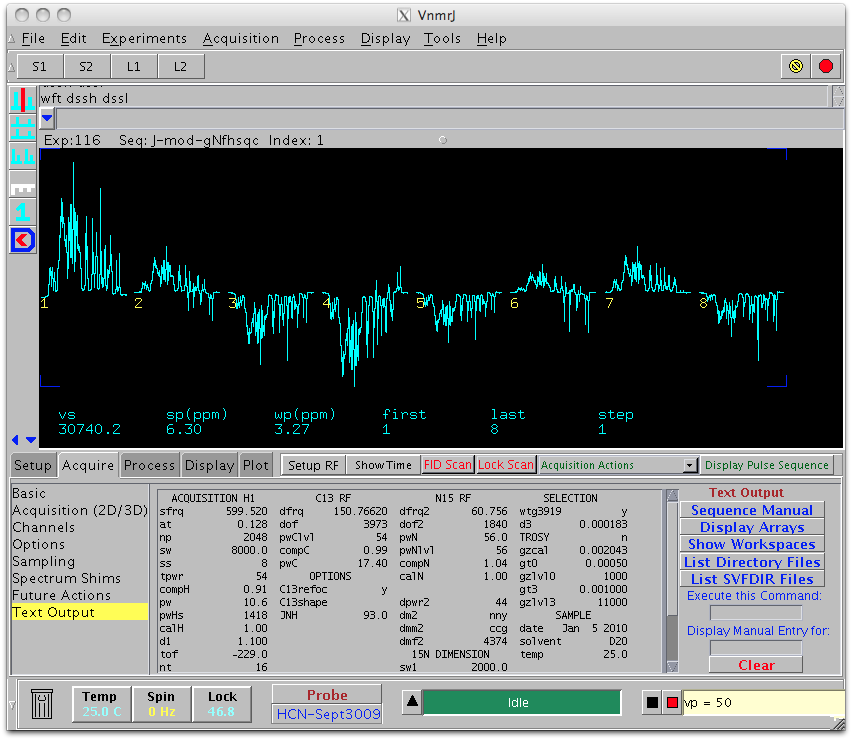
which sets Delta from 0.002 to 0.016, corresponding to J modulating delays from 4 to 32 msec. At least 3 modulation points are needed to extract the coupling constant, along with ¹⁵N T₂ and a parameter related to pulse imperfection. It is recommended to take more than 3 points to get an estimation of experimental error. The maximum delay (32 msec in this case) should be bigger than 3/(2J) ( ~16 msec in case of JNH) to make sure the modulation curve crosses zero at least twice (Tjandra et al). Our simulation shows that the modulation interval should not be close to 1/J (~10ms for JNH),  i.e. the stepsize for Delta should not be close to ~5 msec.  An example of the J-modulation experiment is shown below:

   

General Comments

1. Poor signal to noise (too few scans)
2. Insufficient modulation points (at least 3, but >5 is suggested)
3. Incorrect setting of Delta stepsize (should NOT be around 5ms)
4. Incomplete modulation curve. (at least two zero crossings are required)

ni vs nt

The acquisition time for the indirect dimension of this J-mod method can be shorter than that used for frequency separation methods such as IPAP. It just needs to be long enough to resolve the peaks of interest, and around 30ms is often reasonable. In our experience, linear prediction can be applied without causing noticeable errors.  The time saved from a smaller “ni” can be spent more productively on “nt” to increase S/N.

number of modulation points vs nt

Our simulation shows that these two are equivalent, i.e., one can choose to spend more time averaging each spectrum, or one can use to the time to acquire more modulation points. The errors in both cases are comparable. 

Data Analysis

Data Processing Script: NH-jmod4edit.txt

Split FIDs

If the experiment is acquired in an interleaved fashion, the final fid file contains a series of 2D spectra and thus has to be split into n fids, where n is the number of modulation points. We can send the script for doing this upon request.

Process with nmrPipe

The standard 2D processing for fast HSQC spectra will work. But make sure the same processing is applied to all spectra.

Convert to Sparky

To convert an nmrpipe output file, say test.ft2, to a sparky file called test.ucsf, type:

pipe2ucsf test.ft2 test.ucsf 

This should be applied to all 2D spectra from the J-modulation experiment. To load these ucsf files into a project, a convenient way is to go to the directory that contain these files, and issue:

find `pwd`|grep ucsf|xargs sparky &

This way the full path is associated with each file and thus the project can be reloaded from any initial location after saving.

Convert to NMRViewJ 

For analysis in NMRViewJ, the experiment must be separated into distinct 2D files.  Each must be given a unique name; following the example above there will be 8 files, iso1.ft2 - iso8.ft2, in which iso1.ft2 was collected with a J-modulation delay of 4 ms and iso8.ft2 was collected with a 32 ms delay.  These files will be converted to NMRView format using the following command:

nmrPipe -in iso1.ft2 | pipe2xyz -nv -out iso1.nv

Spectral Measurments 

NMRViewJ 

First, load the files into NMRViewJ.  Open and Draw iso1.nv (Datasets  Open and Draw Dataset).  Adjust the contour level to a reasonable level, and in the Attributes window (right click on spectrum  Attributes) go to the PeakPick tab, chose a name for the list (Protein1) and select the “Pick” button.  Using the cursor (right click, Cursors, select “PeakAdd” or “PeakDelete”) delete noise peaks or add low-intensity peaks.

In a text editor, create a file that specifies the Jmod delays for each specific file.  This time file will present the unique portions of the 2D filenames and the delays (in s).  Remembering there are 8 files (iso1.ft2 - iso8.ft2) with delays from 4-32ms, the time file will look like this:

1. 1 0.004
2. 2 0.008
3. 3 0.012
4. 4 0.016
5. 5 0.020
6. 6 0.024
7. 7 0.028
8. 8 0.032

The data analysis is performed using the Rate Analysis tool (Analysis  Rate Analysis).  In the “Prefix for matrix numbers” box, write the non-unique portion of the filenames (iso).  Select “.nv” for the suffix.  Select the peaklist (Protein1).  Select the button “Load Time File” and load the table created above.

To measure the intensity of each peak click the “Measure All” button.  The graph to the right will show points indicative of a decaying cosine function.   You can click through the peaks to see each peak using the up and down arrows.  Unfortunately, the equation to fit this type of data has not yet been placed in NMRViewJ, but it will be available in a future version.  For now, the data should be saved using the Save Table option and will be analyzed separately.

Sparky 

Create peaks in one of the spectra and center them by the “pc” command. Preferably the one with the shortest modulation delay which has the best S/N. Propagate the peaklist into other spectra. This can be done with the “pa” and “oc” commands with the source spectrum in the front, followed by “op” after bringing the destination spectrum to the front. It is not necessary to re-center the peaks in each spectrum. 

To save the peak lists containing the intensities, do an “lt”. In “Options”, check “Data Height” so that the output contains the intensities for each peak.

Curve Fitting

With the data in a table format of Intensity vs Delay for each peak, the following equation may be fit to these data to determine the Jmod values:

f(x) = c * (-a + cos(3.14159*2*j*x))*exp(-2*x/t)

where a is a variable accounting for imperfection of pi pulses during the experiment (usually 0 < a < 0.05), c is the initial intensity of the peak, j is the one-bond H-N J-coupling value in Hz and t is the T₂ relaxation rate.

This equation may be fit individually or in a batch mode using any common curve-fitting algorithm.